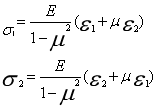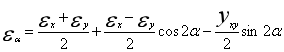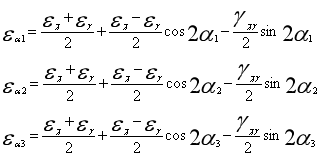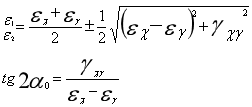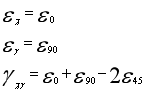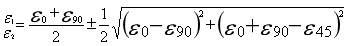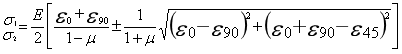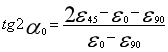應力與應變(bian)換算關(guan)系(xi)

用(yong)電阻應變(bian)片測(ce)出的(de)是構件(jian)上某壹(yi)點處沿某(mou)壹(yi)方(fang)向的(de)線(xian)應變(bian)，須(xu)經(jing)過應變(bian)-應力換算才能(neng)得(de)到(dao)主應力。不同的(de)應力狀態有(you)不同的(de)換算關(guan)系(xi)，下(xia)面(mian)聚(ju)航(hang)科(ke)技就(jiu)給(gei)大家(jia)介紹壹(yi)下(xia)平面(mian)應力狀態時(shi)的(de)應變(bian)-應力換算關(guan)系(xi)。

單(dan)向(xiang)應力狀態

構件(jian)在(zai)外力作(zuo)用(yong)下(xia)，若被測點為(wei)單(dan)向(xiang)應力狀態，則(ze)主應力方(fang)向已(yi)知，只有主應力σ是未知量，可(ke)沿(yan)主應力σ的(de)方(fang)向粘(zhan)貼(tie)壹(yi)個應變(bian)片，測(ce)得(de)主應變(bian)ε後(hou)，由胡(hu)克(ke)定律

σ=Eε  （1）

即可(ke)求的(de)主應力σ。式(shi)中(zhong)E為(wei)被測構件(jian)材(cai)料的(de)彈性模量。

已知主應力方(fang)向的(de)二向(xiang)應力狀態

受內(nei)壓(ya)力作(zuo)用(yong)的(de)薄壁(bi)容器(qi)，其表面(mian)各(ge)點為(wei)已知主應力方(fang)向的(de)二向(xiang)應力狀態，有(you)主應力σ₁、σ₂兩個未知量，可(ke)沿(yan)主應力方(fang)向，粘(zhan)貼(tie)互相垂(chui)直(zhi)的(de)兩個應變(bian)片（組(zu)成二(er)軸90°應變(bian)花(hua)），測得(de)主應變(bian)ε₁和ε₂，由廣(guang)義(yi)胡(hu)克(ke)定律

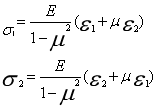    （2）

即可(ke)求的(de)主應力σ₁、σ₂。式(shi)中(zhong)μ為(wei)被測構件(jian)材(cai)料的(de)泊(bo)松(song)比。

未知主應力方(fang)向的(de)二向(xiang)應力狀態

對於(yu)形狀和(he)受(shou)力情況比(bi)較(jiao)復雜的(de)構件(jian)，除(chu)了(le)被測點兩個主應力值未知外，主應力方(fang)向也是未知的(de)，即存(cun)在(zai)σ₁、σ₂和σ₀三(san)個未知量。此(ci)時(shi)，可(ke)以(yi)在(zai)該點(dian)沿著(zhe)三(san)個不(bu)同方(fang)向粘(zhan)貼(tie)三(san)個應變(bian)片，根據(ju)測得(de)的(de)應變(bian)值(zhi)換算成主應力值，換算原理(li)如(ru)下(xia)：

在(zai)構件(jian)上，有壹(yi)未知主應力大小(xiao)和方(fang)向的(de)測點(dian)，在(zai)該測(ce)點處任意(yi)選(xuan)定直(zhi)角坐標(biao)X0Y，並(bing)在(zai)與X軸成α₁、α₂和α₃夾角方(fang)向上各粘貼(tie)壹(yi)片應變(bian)片。由(you)三(san)個應變(bian)片分(fen)別測(ce)得(de)這三(san)個方(fang)向上的(de)應變(bian)ε_α1和ε_α2和ε_α3。另(ling)外(wai)由二向應力狀態的(de)應變(bian)分(fen)析可(ke)知，若已知該測定0處沿坐標(biao)軸(zhou)方(fang)向的(de)線(xian)應變(bian)ε_x、ε_y和剪(jian)應變(bian)Y_xy，則該點(dian)處任意(yi)方(fang)向的(de)線(xian)應變(bian)ε_α的(de)計(ji)算(suan)公(gong)式(shi)為(wei)

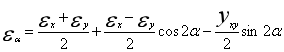    （3）

式(shi)中(zhong)ε_x、ε_y和ε_α以伸長(chang)為(wei)正，Y_xy以直(zhi)角*大(da)為(wei)正。這(zhe)樣(yang)該測點(dian)處三(san)個方(fang)向上的(de)應變(bian)片測(ce)得(de)的(de)應變(bian)ε_α1、ε_α2和ε_α3與任意(yi)方(fang)向上的(de)線(xian)應變(bian)ε_α便有

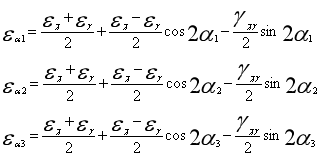    （4）

這樣由(you)公(gong)式(shi)（3）就(jiu)可(ke)解(jie)出ε_x、ε_y和Y_xy。

由材(cai)料力學知，已知ε_x、ε_y和Y_xy，則該測(ce)點處的(de)主應變(bian)和(he)主應變(bian)方(fang)向與X軸的(de)夾角(jiao)α₀就(jiu)可(ke)由(you)下(xia)式(shi)計(ji)算(suan)得(de)到(dao)。

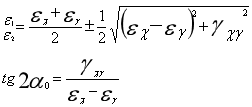    （5）

*後，由公(gong)式(shi)（2）廣(guang)義(yi)胡(hu)克(ke)定律，即可(ke)求得(de)主應力σ₁、σ₂，主應變(bian)方(fang)向α₀即為(wei)主應力方(fang)向。

三(san)個應變(bian)片之(zhi)間(jian)的(de)夾角(jiao)可(ke)以(yi)任意(yi)設(she)定，但(dan)是為(wei)了(le)計(ji)算(suan)方(fang)便，壹(yi)般會選(xuan)擇某些(xie)特定角(jiao)度(du)，如(ru)0°、45°、60°、90°。電阻應變(bian)片中(zhong)的(de)應變(bian)花(hua)就(jiu)是根據(ju)此(ci)測(ce)試(shi)要(yao)求設計(ji)生產的(de)。

對於(yu)不同形式(shi)的(de)應變(bian)花(hua)均可(ke)由(you)測量結(jie)果(guo)ε_αi（i=1，2，3），根據(ju)公(gong)式(shi)（2）、（3）、（4）導出被測點的(de)主應力和主應力方(fang)向的(de)計(ji)算(suan)公(gong)式(shi)。

下(xia)面(mian)推(tui)導應用(yong)*廣(guang)的(de)三(san)軸45°應變(bian)花(hua)的(de)應變(bian)-應力換算關(guan)系(xi)。

三(san)軸45°應變(bian)花(hua)α₁=0°，α₂=45°，α₃=90°，若測出的(de)應變(bian)相(xiang)應為(wei)ε₀，ε₄₅，ε₉₀，將他(ta)們代入(ru)公(gong)式(shi)（3），可(ke)解(jie)得(de)

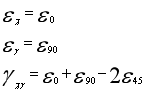     （6）

根據(ju)公(gong)式(shi)（4），即(ji)可(ke)得(de)到(dao)主應力計(ji)算(suan)公(gong)式(shi)

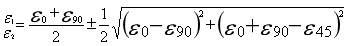   （7）

再將上式(shi)代入(ru)公(gong)式(shi)（2），即(ji)可(ke)得(de)到(dao)主應力計(ji)算(suan)公(gong)式(shi)

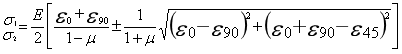  （8）

因主應力方(fang)向與主應變(bian)方(fang)向壹(yi)致(zhi)，故可(ke)由(you)公(gong)式(shi)（4）得(de)到(dao)主應力方(fang)向計(ji)算(suan)公(gong)式(shi)

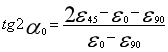    （9）

以上就(jiu)是應力應變(bian)換算關(guan)系(xi)的(de)介紹，如(ru)果(guo)您(nin)還有其他(ta)的(de)疑(yi)問，可(ke)直(zhi)接咨(zi)詢聚(ju)航(hang)科(ke)技，我們歡(huan)迎(ying)您(nin)的(de)咨詢(xun)。